Question

find the value of each trigonometric ratio. Express it as a fraction (ratio) and then divide your fraction and express as a decimal rounded to 4 decimal places

Answer 1

The tangent can be calculated with the following expression:

`\tan (\alpha)=\frac{\text{ opposite cathetus}}{\text{ adjacent cathetus}}`

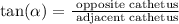
Where alpha is the angle we want to use, the opposite cathetus is the length of the side that is farther from the angle and the adjacent cathetus is the length of the side that is closer to the angle. We need to calculate the tangent for the C vertex, so the opposite cathetus is 28 and the adjacent cathetus is 21. We have:

`\tan (C)=(28)/(21)=(4)/(3)=1.3333`

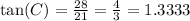
The tangent is 4/3 or 1.3333.

The sine can be calculated with the following expression:

`\sin (\alpha)=\frac{\text{ opposite cathetus}}{\text{ hypothenuse}}`

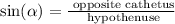
The hypothenuse is the side facing the right angle directly. For this question the hypothenuse is 35. We have:

`\sin (C)=(28)/(45)=0.6222`

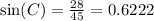
The sine is 28/45 or 0.6222.

The cosine can be calculated with the following expression:

`\cos (\alpha)=\frac{\text{ adjacent cathetus}}{\text{ hypothenuse}}`

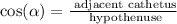
Applying the data from the problem we have:

`\cos (C)=(21)/(35)=0.6`

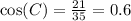
The cosine is 21/35 or 0.6.