Question

1. M and N are two groups of rabbits.The initial population of M is 5 rabbits, and the population doubles each year.• The initial population of N is 10 rabbits, and the population increases linearly eachyear.If both populations are the same after 3 years, what is the rate ofchange of the population of N?A 40 rabbits per yearB. 35 rabbits per yearc. 20 rabbits per yearD. 10 rabbits per year 16 saved After

Answer 1

The two groups of rabbits grow exponentially and linearly respectively.

For group M with an exponential growth model where the population doubles each year, we have the model to be:

`P(t)=5(2)^t`

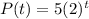
For group N with a linear model, we have the model to be:

`P(t)=10+mt`

where m is the rate of change of the population of rabbits.

After 3 years, both populations are equal. Hence, we can put t = 3 into the equations and equate them to one another:

`5(2)^3=10+3m`

Solving for m, we have:

`\begin{gathered} 40=10+3m \\ 3m=40-10=30 \\ m=(30)/(3) \\ m=10 \end{gathered}`

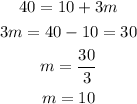
OPTION D is correct.