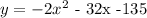Question

What is the equation of a parabola with vertex (-8, – 7) that passesthrough (-7, -9)?

Answer 1

Here in this question, we are to find the equation of the parabola.

Generally, the equation of a parabola is in the form;

`y=a(x-h)^2\text{ + k}`

The term (h,k) represent the coordinates of the vertex.

In this case, h = -8 and k = -7

The term 'a' is simply referred to as a multipier.

Now, we insert the coordinates of the vertex into the equation and we have the following expression;

`y=a(x-(-8))^2+(-7)`

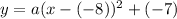
and we have y = a(x + 8)^2 -7

To finally get the equation, we will need to calculate the value of the multiplier. The value of the multiplier can simply be calculated by substituting the value of x and y in the point through which the parabola passes.

Hence, we are substituting the values x = -7 and y = -9

So, we have;

-9 = a(-7+8)^2 -7

-9 = a(1)^2 -7

-9 = a - 7

a = -9 + 7 = -2

So our equation becomes;

y = -2(x+8)^2 - 7

we simply finish this by expanding the equation;

y = -2(x+8)(x+8) - 7

y = -2(x^2 + 16x + 64) -7

y = -2x^2 - 32x -128 -7

y = -2x^2 -32x -135

The equation of a parabola with vertex (-8, – 7) that passes through (-7, -9) is ;

`y=-2x^2\text{ - 32x -135}`