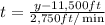Question

An airplane is flying at a steady elevation of 1 1,500 feet. The pilots of the airplane are informed they are approaching a storm, and they will need to ascend to an elevation of 33.000 feet to avoid flying through the storm. As soon as the pilots received the information about the storm, they immediately began to ascend at a constant rate. After 2 minutes, the airplane reached an elevation of 17,000 feet Part A Write an equation that could represent the amount of time it takes the airplane to ascend to the elevation necessary to avoid flying through the storm. Use t to represent the amount of time, in minutes, spent ascending

Answer 1

Consider that the motion of the airplane is uniform, that is, the speed of the airplane is constant. Use the following formula:

`t=(y-y_0)/(v)`

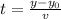
where v is the speed of the airplane, y0 is the initial height of the airplane respect to the ground and y is the height of the airplane after t minutes.

Consider that the airplane travels from 11,500 feet to 17,000 feet in 2 min. Then, the airplane travels 17,000 - 11,500 = 5,500 in 120 s.

The speed of the airplane on this interval is:

v = 5,500 ft/2 min = 2,750 ft/min

The equation for the time t is:

`t=(y-11,500ft)/(2,750ft/\min )`