Question

A fruit company delivers its fruit in two types of boxes: large and small. A delivery of 6 large boxes and 5 small boxes has a total weight of 180 kilograms. A delivery of 2 large boxes and 3 small boxes has a total weight of 78 kilograms. How much does each type of box weigh?Weight of each large box:Weight of each small box:Solve by using system of linear equations.

Answer 1

The Solution:

Let the weight of a large box be x.

And the weight of a small box be y.

Given:

Delivery of 6 large boxes and 5 small boxes has a total weight of 180 kilograms.

`6x+5y=180...eqn(1)`

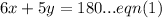
Delivery of 2 large boxes and 3 small boxes has a total weight of 78 kilograms.

`2x+3y=78...eqn(2)`

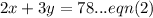
Solve the system of equations by the elimination method of simultaneous equations.

Step 1:

Multiply through eqn(2) by 3 to make the coefficients of x in both equations equal.

`\begin{gathered} 3(2x+3y=78)=6x+9y=234 \\ 6x+9y=234...eqn(3) \end{gathered}`

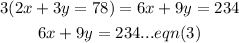
Step 2:

To eliminate the term in x, we shall subtract eqn(1) from eqn(3).

`\begin{gathered} 6x+9y=234...eqn(3) \\ -(6x+5y=180)...eqn(1) \\ -------------- \\ 4y=54_ \\ \\ Divide\text{ both sides by 4, we get} \\ y=(54)/(4)=13.5\text{ kilograms} \end{gathered}`

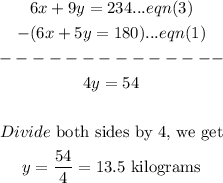
Step 3:

Substitute 13.5 for y in eqn(2) to get x.

`\begin{gathered} 2x+3(13.5)=78 \\ 2x=78-40.5 \\ 2x=37.5 \end{gathered}`

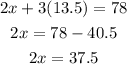
Dividing both sides by 2, we get

`x=(37.5)/(2)=18.75\text{ kilograms}`

Therefore, the correct answers are:

The weight of each large box = 18.75 kilograms

The weight of each small box = 13.5 kilograms