Step-by-step explanation:
The diagonals of a rectangle are congruent and the intersecting point is the middle point of both:
Therefore, for this problem DZ ≅ BZ and DB = DZ + BZ. Also DB ≅ AC. Since DZ ≅ BZ
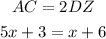
Solving for x:
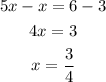
To find AC we just have to replace x = 3/4 into the expression for its length:
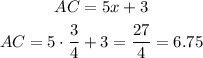
Answer:
AC = 6.75