Question

015 (part 1 of 3) 10.0 pointsA model rocket is launched straight upwardwith an initial speed of 49.7 m/s. It acceler-ates with a constant upward acceleration of2.69 m/s2 until its engines stop at an altitudeof 217.3 m.What is the maximum height reached bythe rocket?Answer in units of m.ray.Баto

Answer 1

We know that

• The initial speed is 49.7 m/s.

,

• The acceleration is 2.69 m/s^2.

,

• The altitude is 217.3 m.

,

• The final velocity is zero because it stops at a certain point.

To find the maximum height, we use the following equation.

`v^2_f=v^2_0+2ah`

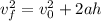
Using the given magnitudes, we have the following.

`\begin{gathered} 0=(49.7((m)/(s)))^2+2(-2.69((m)/(s^2)))h \\ -2,470.09((m^2)/(s^2))=-5.38((m)/(s^2))h \\ h=(-2,470.09((m^2)/(s^2)))/(-5.38((m)/(s^2))) \\ h\approx459.12m \end{gathered}`

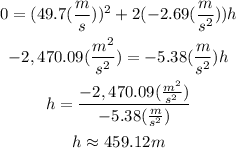
Therefore, the maximum height is 459.12 meters. (a)

Then, we find the time spent to reach the maximum height.

`v_f=v_0+at`

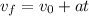
Let's replace the given magnitudes to find the time t.

`\begin{gathered} 0=49.7((m)/(s))-2.69((m)/(s^2))t \\ -49.7((m)/(s))=-2.69((m)/(s^2))t \\ t=(-49.7((m)/(s)))/(-2.69((m)/(s^2))) \\ t\approx18.48\sec \end{gathered}`

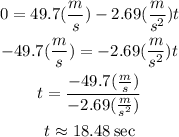
Therefore, the time spent was 18.48 seconds. (b)

At last, to find the total time the rocket spent in the air (not just to reach maximum altitude), we have to multiply the time we already calculated by two because that represents the total time from the beginning of the movement to the end of it (reaching ground again).

`t_(total)=2\cdot18.48\sec =36.96\sec`

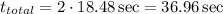
Therefore, the rocket spent 36.96 seconds in the air. (c)