Question

If ABC was translated 2 units right and 4 units down, then rotated 90 degrees clockwise about the orgin, where would point A be located?

Answer 1

Since we a looking for the position of A we can work on Point A without drawing the diagram.

STEP 1

We pick out the coordinates of A. This is given as (5,4) this implies that the position of A on the cartesian plane is (5,4)

STEP 2:

If we translate ABC by 2 units to the right, this implies we add two to the x coordinate of A

For example, (x,y) becomes (x+2,y)

Therefore

`(5,4)\text{ becomes (7,4)}`

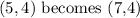
STEP 3

If we translate ABC by 4 units down, this implies we subtract 4 from the y coordinate of A

For example, (x,y) becomes (x,y-4)

Therefore

`(7,4)\text{ becomes(7,0)}`

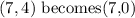
STEP 4

If we rotate by 90 degrees clockwise this implies that we interchange the x coordinate with the y coordinate and attach a minus to the new y coordinate.

For example, (x,y) becomes (y,-x)

Therefore,

`(7,0)\text{ becomes (0,-7)}`

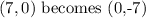
Therefore, the final location for A is (0,-7)