Question

To demonstrate probabilities, a mathematics teacher had students draw cards from a bag which contained 26 red cards and26 black cards. During class, the bag was dropped, and 4 red cards and 2 black cards were lost.Tell whether the loss of cards changes the probability of drawing a black card from the bag.If so, was the probability increased or decreased? Support your answer by calculating the probability for each situation.

Answer 1

The probability of an event is given by the following formula:

`P(X)=\frac{Number\text{ of favorable outcomes to X}}{\text{Total number of possible outcomes}}`

The total number of possible outcomes is the total number of red and black cards in the bag.

The favorable outcomes to drawing a black card in the first situation are 26 (because there are 26 black cards).

The probability of drawing a black card before the bag was dropped was:

`P(\text{black card)=}(26)/(26+26)=(26)/(52)=0.5`

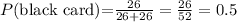
After the bag was dropped, the total number of cards is:

Red cards= 26-4=22 and Black cards=26-2=24 cards.

Total number of cards=22+24=46.

The probability of drawing a black card after the bag was dropped is:

`P(\text{black card)=}(24)/(46)=0.52`

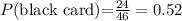
Thus, the probability of drawing a black card from the bag increased.