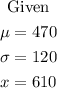
Find the z-score of Sheila's score.
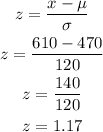
Since we are looking for the percent of takers that earned a higher score then Sheila, find P( z > 1.17)
Looking at the value to the left of the z-score we have
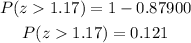
Multiply by 100% and we get
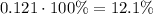
Rounding to the nearest whole number, the percent of takers who earned a higher score than Sheila is 12%