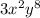Question

help with question 2?? i have a lot of work and want to get this done:/Fill the missing portion of each product to make the equation an identity.

Answer 1

To answer this question, we need to divide the left part of the equation by the right part of the equation. After doing that, we will find the other necessary factor that we need to make the equation an identity, that is, both parts will be equal for every value of x.

We need to apply the rule of exponents for each case. The next rule will be very useful here:

`(x^m)/(x^n)=x^(m-n)`

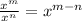
And this is called the Quotient Rule for Exponents.

Then, we have:

Part a:

`(18x^6)/(3x^2)=(18)/(3)\cdot(x^(6-2))=6x^4`

Now, we can confirm that:

`18x^6=3x^2\cdot6x^4=(3\cdot6)(x^{2+4_{}})=18x^6\Rightarrow18x^6=18x^6`

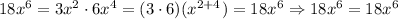
And we can similarly proceed with the other cases.

Part b:

`(40x^2y^7)/(8xy^2)=(40)/(8)(x^(2-1))(y^(7-2))=5xy^5`

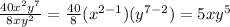
To check this:

`40x^2y^7=8xy^2\cdot5xy^5=(8\cdot5)(x^{1+1_{}_{}_{}})(y^{2+5_{}}_{})=40x^2y^7\Rightarrow40x^2y^7=40x^2y^7`

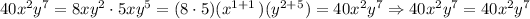
Part c:

`(24x^6)/(-3x^2)=(24)/(-3)(x^(6-2))=-8x^4`

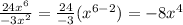
Then, we have that:

`24x^6=-3x^2\cdot(-8x^4)=(-3\cdot-8)x^{2+4_{}}=24x^6\Rightarrow24x^6=24x^6`

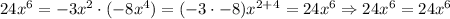
Part d:

`-(48x^4y^(10))/(-16x^2y^2)=(-48)/(-16)(x^(4-2)_{})(y^(10-2))=3x^2y^8`

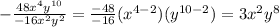
Then, to confirm this result:

`-48x^4y^(10)=-16x^2y^2\cdot(3x^2y^8)=(-16\cdot3)\cdot x^{2+2_{}}\cdot y^{2+8_{}_{}}=-48x^4y^(10)`

In summary, we have to fill the missing portion with the following factors:

Part a:

`6x^4`

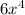
Part b:

`5xy^5`

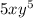
Part c:

`-8x^4`

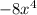
Part d:

`3x^2y^8`