Answer:
![\begin{gathered} d)\text{The angles in ABC have the same measures as the angles in DEF} \\ \text{The radio of corresponding sides lengths are equal }to\text{ each other} \\ \text{The triangles are similar} \\ c)\text{ }(AB)/(DE)=(12)/(6)=2 \\ (BC)/(EF)=(6)/(3)=2 \\ (CA)/(FD)=(10)/(5)=2 \end{gathered}]()
Explanation:
Make a diagram with the given information:
Since the sum of all intern angles of a triangle must add up to 180°, and you have two angles of each one:
![\begin{gathered} Assuming you did the measure of the lengths correctly with the rule:[tex]\begin{gathered} AB=12,\text{ B}C=6,\text{ }CA=10 \\ DE=6,\text{ }EF=3,\text{ FD=}5 \\ \end{gathered}]()
c) The ratio for the sides is the relation between the sides:
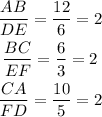
d) For the given statements:
![\begin{gathered} \text{The angles in ABC have the same measures as the angles in DEF} \\ \text{The radio of corresponding sides lengths are equal }to\text{ each other} \\ \text{The triangles are similar} \end{gathered}]()