Question

What is the slope of the line created by this equation?Round your answer out to two decimal places.2x+5y=10

Answer 1

The general equation of a line id expressed as

`\begin{gathered} y\text{ = mx + c ---- equation 1} \\ where \\ m\Rightarrow slope\text{ of the line} \\ c\Rightarrow y-intercept\text{ of the line} \end{gathered}`

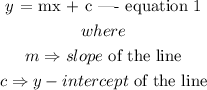
Given that a line equation to be

`2x\text{ + 5y = 10 ---- equation 2}`

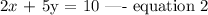
Step 1:

From equation 2, make y the subject of the formula.

`\begin{gathered} 2x+5y\text{ = 10} \\ subtract\text{ }2x\text{ from both sides of the equation} \\ 2x-2x+5y\text{ = 10-2x} \\ 5y\text{ = 10 - 2x} \\ divide\text{ both sides of the equation by the coefficient of y, which is 5.} \\ \text{thus,} \\ (5y)/(5)\text{ = }\frac{\text{10-2x}}{5} \\ \Rightarrow y\text{ = 2-}(2)/(5)x\text{ ---- equation 3} \\ \end{gathered}`

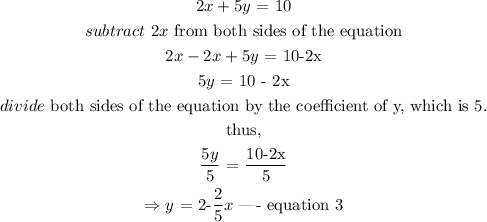
Step 2:

Compare equations 1 and 3.

`\begin{gathered} \text{Equation 1: y = mx + c} \\ \text{Equation 3: y = -}(2)/(5)x+2 \end{gathered}`

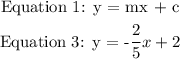
comparing both equations,

`m\text{ = -}(2)/(5)\text{ = -0.40, c=2}`

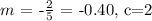
Hence, the slope of the line is -0.40 (2 decimal places).