Question

Find an equation of the line L, where L is perpendicular to and passes through the point

Answer 1

We have to find the equation of the line "L" that is perpendicular to y=3x and passes through the point (1,3)

First let's find the slope of the perpendicular line, the slope of the line with equation y = 3 x is 3. If we multiply the slopes of two perpendicular lines, we get -1.

`3x\cdot-(1)/(3)=-1`

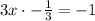
Therefore the slope of our perpendicular line "L" is -1/3

Second, we will make sure that the slope passes through the point (1,3)

Now use the intercept-slope form to find the equation

`y-y_1=m(x_{}-x_1)`

In this case, y1 = 3 and x1 = 1 and remember that m = -1/3, we substitute these values into the equation and operate

`\begin{gathered} y-3=-(1)/(3)(x-1) \\ y-3=-(1)/(3)x+(1)/(3) \\ \end{gathered}`

Add 3 units to both sides

`\begin{gathered} y-3+3=-(1)/(3)x+(1)/(3)+3 \\ y=-(1)/(3)x+(10)/(3) \end{gathered}`

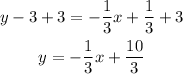
The last result is our line "L" which is perpendicular to y=3x and passes through the point (1,3).

This is the answer