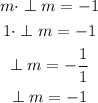Question

Use Midpoint and Slope Formulas to complete the tables below.1. Find the midpoint of RP, given the coordinates R (5, 8) and P (3, 6).m:Il m:I m:Midpoint:

Answer 1

The midpoint formula for a segment is:

`x_m,y_(_m)=((x_1+x_2))/(2),((y_1+y_2))/(2)`

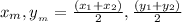
apply to points R and P

`\begin{gathered} x_m,y_m=((5+3))/(2),((8+6))/(2) \\ x_m,y_m=(8)/(2),(14)/(2) \\ x_m,y_m=(4,7) \end{gathered}`

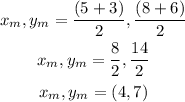
using the definition of slope find the slope of the segment

`m=(y_2-y_1)/(x_2-x_1)`

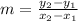
apply to points R and P

`\begin{gathered} m=(8-6)/(5-3) \\ m=(2)/(2) \\ m=1 \end{gathered}`

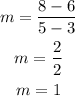
to lines are parallel when the slopes are the same

`\mleft\Vert m=1\mright?`

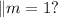
two lines are perpendicular when the product of the slopes is equal to -1

`\begin{gathered} m\cdot\perp m=-1 \\ 1\cdot\perp m=-1 \\ \perp m=-(1)/(1) \\ \perp m=-1 \end{gathered}`