Question

How many moles of solute are required to make 3.0L of a 2.0M solution

Answer 1

6.0 moles.

Step-by-step explanation:

To solve this problem, we have to use the molarity formula. Remember that the molarity (M) of a solution is the number of moles of solute dissolved in one liter of solution:

`Molarity\text{ \lparen M\rparen=}\frac{moles\text{ of solute}}{liter\text{s of solution}}=(mol)/(L).`

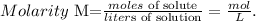
We want to find 'moles of solute', so we have to solve for this unknown value and replace the given data (molarity = 2.0 M, liters of solution = 3.0 L):

`\begin{gathered} Moles\text{ of solute=molarity}\cdot liters\text{ of solution,} \\ \\ Moles\text{ of solute=2.0 M}\cdot3.0\text{ L,} \\ \\ Moles\text{ of solute= 6.0 moles.} \end{gathered}`

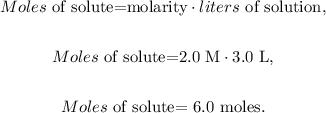
The answer would be that we require 6.0 moles to prepare the wanted solution.