Question

The table provides various values, including all minimums and maximums, of a cosine function f (x) on the interval [−π, π].The table shows from x = -pi to x=pi and f(x) comes back at the same value at - pi and piWhat is the period of the function?

Answer 1

`\pi`

Step-by-step explanation

The distance between the repetition of any function is called the period of the function( this is not the graph of the function, it is another periodic function)

therefore, to find the period, find the distance between 2 identical values for y, so

`\text{period}=X_2-X_1`

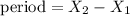
so

`\text{period}=X_2-X_1`

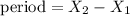
so, let

`\begin{gathered} X_2=(\pi)/(2) \\ X_1=-(\pi)/(2) \end{gathered}`

hence

`\begin{gathered} \text{period}=X_2-X_1 \\ \text{period}=(\pi)/(2)-(-(\pi)/(2))=(\pi)/(2)+(\pi)/(2)=\pi \end{gathered}`

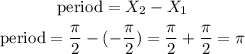
therefore, the answer is:

`\pi`

I hope this helps you