Question

Determine whether the graph of the function is symmetric with respect to the y-axis, the origin, or neither. f(x)= xcubed - 2x

Answer 1

we have the function

`f\mleft(x\mright)=x^3-2x`

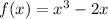
part 1

Verify if the function is symmetric with respect to the y-axis

A graph is symmetric with the y-axis

if

f(x)=f(-x)

so

`\begin{gathered} f(-x)=(-x)^3-2(-x) \\ f(-x)=-x^3+2x \\ therefore \\ f(x)\\e\text{ f\lparen-x\rparen} \end{gathered}`

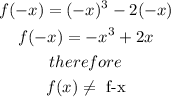
The graph is not symmetric with respect to the y-axis

part 2

Verify if the function is symmetric with respect to the x-axis

A graph is symmetric with the x-axis

If

f(x)=-f(x)

so

`\begin{gathered} -f(x)=-(x^3-2x) \\ -f(x)=-x^3+2x \\ therefore \\ f(x)\\e-f(x) \end{gathered}`

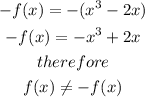
The graph is not symmetric with respect to the x-axis

Part 3

Verify if the function is symmetric with respect to the origin

A graph is symmetric with the origin

if

f(x)=-f(-x)

so

`\begin{gathered} -f(-x)=-[(-x)^3-2(-x)] \\ -f(-x)=-[-x^3+2x] \\ -f(-x)=x^3-2x \\ therefore \\ f(x)=-f(-x) \end{gathered}`

therefore

The answer is

The graph is symmetric with respect to the origin