Question

The driver of a car slams on the brakes and skids to a stop in 19 m. If the rate of acceleration is -3.1 m/s per second, how fast was the car moving before the car begins to stop? Round to 4 decimals if necessary

Answer 1

10.8537 m/s

Step-by-step explanation

Given:

• The distance the car skid for after braking, x = 19 m

,

• The acceleration of the car, a = -3.1 m/s

Find:

• The speed of the car before it begins to stop, u

The speed of an object moving with constant acceleration a during a time t is,

`v=u+at`

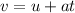
And the distance it moves is,

`x=ut+(1)/(2)at^2`

Taking the motion of the car after the driver slammed on the brakes, then the final speed would be 0, and the initial speed, u, would be the one we have to find,

`u=-at`

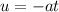
So, the distance the car travels is,

`x=-at\cdot t+(1)/(2)at^2=-at^2+(1)/(2)at^2=-(1)/(2)at^2`

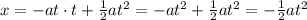
With this equation, we can find the time it took the car to stop. Solving for t,

`t=\sqrt{(2x)/(-a)}`

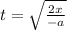
Replace the known values and solve,

`t=\sqrt{(2\cdot19m)/(-(-3.1)m/s^2)}\approx3.5012s`

Replace this value in the equation for the initial speed,

`u=-at=-(-3.1)m/s^2\cdot3.5012s\approx10.8537m/s`

Hence, the car was moving at 10.8537 m/s, rounded to four decimal places, when it began to stop.