1 Answer

Bob Mazanec · Answer 1 · 2023-01-16T02:28:53+0000

Answer: Provided the function, we have to answer the questions (a) to (f), the function is as follows:

$f(x)=x^3+3x^2-105x+24\rightarrow(1)$

(a) The first derivative of (1) is as follows:

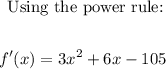
$\begin{gathered} \text{ Using the power rule:} \\ \\ f^(\prime)(x)=3x^2+6x-105 \end{gathered}$

(b) The second derivative is calculated using the same method as in part (a), only the difference is that it is calculated twice:

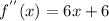
$f^{^(\prime)^(\prime)}(x)=6x+6$

(c) The interval where the function is increasing can be found by inspecting the graph of the original function or the equation (1):

The plot is as follows:

The interval on which the function is increasing is:

$x=[-\infty,-7]\text{ and }x=[5,\infty]$

(d) Similarly, the decreasing interval is as follows:

(e) Concave upward:

$x=[-7,+\infty]$

(f) Concave downward:

Similarly, the concave downward is on the following interval:

$x=[-\infty,-7]$

Please log in or register to add a comment.