Question

A pole that is 3.1 m talk casts a shadow that is 1.25

Answer 1

A pole of actual height, H, 3.1m casts a shadow of 1.25m

Let the height of the building be x which casted a shadow of height 50,25m

The ratio of the actual height to the shadow height of the pole is

`\text{Ratio}=\frac{\text{Actual height of pole}}{Shadow\text{ height of pole}}=(3.1)/(1.25)`

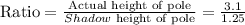
The ratio of the actual height to the shadow height of the building is

`\text{Ratio}=\frac{\text{Actual height of building}}{Shadow\text{ height of building}}=(x)/(50.25)`

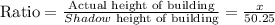
The proportion of both ratio is

`(3.1)/(1.25)=(x)/(50.25)`

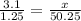
Crossmultiply to find the value of x

`\begin{gathered} (3.1)/(1.25)=(x)/(50.25) \\ 1.25x=3.1*50.25 \\ \text{Divide both sides by 1.25} \\ (1.25x)/(1.25)=(155.775)/(1.25) \\ x=124.62m \\ x=125m\text{ (nearest meter}) \end{gathered}`

Hence, the height of the building is 125m (nearest meter)