Question

Under the pink line is the answer, elaborate and explain

Answer 1

A continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. A function is said to be continuous in a point if the one-sided limits on this points are equal to the actual function value on that point.

Let's analyze the one-sided limits at x = 1.

`\lim_(x\to1^-)f(x)=\lim_(x\to1^+)f(x)=3\\e f(1)=4`

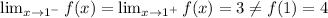
Since the limits are not equal to the function value, the function is not continuous at x = 1. The next point of possible discontinuity would be at x = 2.

We have for x = 2 the following limits:

`\begin{gathered} \lim_(x\to2^-)f(x)=2=f(2) \\ \lim_(x\to2^+)f(x)=3\\e f(2) \end{gathered}`

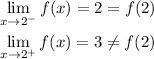
Here, the one-sided limit coming from the left is equal to the function value at x = 2, but the one sided limit coming from the right isn't, therefore, the function is only continuous from the left at x = 2.

Reproducing the same analysis for the other points, we get our answer. Since the function is not defined at x = 0, x = 3, and x = 4, the function can't be continuous on those points.