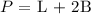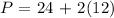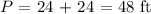Question

You are designing a rectangular garden for the city park. The garden is to have an area of 288 square feet, but you want to minimize the amount of fencing that you need to surround the garden. One length of the garden will not have a fence. How many feet of fencing do you need to surround the garden?

Answer 1

Answer: The feet of fencing needed to surround the garden = 48 ft

The Area of the rectangular garden = 288 ft

Area of a rectangle, A = Length * Breadth

Let the length = L

and the breadth = B

A = LB

288 = LB

B = 288/L

Perimeter, P = 2(L+B) = 2L + 2B

But since one length of the garden will not have a fence, the perimeter of the fence will be given as:

Perimeter, P= L +2B

`P\text{ = L + }(2(288))/(L)`

`P\text{ = L + }(576)/(L)`

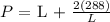
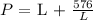
Differentiate the perimeter, P

`(dP)/(dL)\text{ = 1 - }(576)/(L^2)`

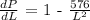
Since the amount of fencing should be minimized, dP/dL = 0

`0\text{ = 1 - }(576)/(L^2)`

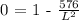
Multiply through by L^2

`L^2\text{ - 576 = 0}`
`L^2\text{ = 576}`
`L\text{ = }24\text{ ft}`

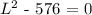
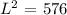
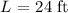
The Breadth of the fence will be given as:

`B\text{ = }(288)/(L)\text{ = }(288)/(24)\text{ = }12\text{ ft}`

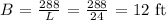
The feet of fencing needed to surround the fence will be the perimeter of the rectangular fence:

`P\text{ = L + 2B}`
`P\text{ = 24 + 2(12)}`
`P\text{ = 24 + 24 = 48 ft}`