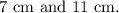Question

The perimeter of a rectangle is 36cm. The length of the rectangle is 4cm more than its width. Find the dimensions of the rectangle.

Answer 1

Given:

the perimeter of a rectangle is

`36\text{ cm.}`

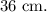
The length of the rectangle is 4 cm more than its width.

Required:

We have to find the dimension of the rectangle which is the length and width of the rectangle.

Step-by-step explanation:

Let the width of the rectangle be

`x\text{ cm.}`

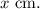
Then the length of the rectangle will be

`(x+4)\text{ cm.}`

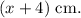
Now we use the formula for the perimeter of a rectangle to find the required answer.

Then proceed as follows:

`\begin{gathered} 2(\text{ length}+\text{ width\rparen}=36 \\ \Rightarrow2\lbrace(x+4)+x\rbrace=36 \end{gathered}`
`\begin{gathered} \Rightarrow\lbrace x+4+x\rbrace=(36)/(2) \\ \Rightarrow2x+4=18 \end{gathered}`
`\begin{gathered} \Rightarrow2x=18-4 \\ \Rightarrow2x=14 \end{gathered}`
`\begin{gathered} \Rightarrow x=(14)/(2) \\ \Rightarrow x=7\text{ cm.} \end{gathered}`

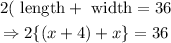
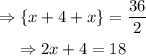
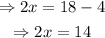
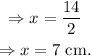
Therefore the width of the rectangle is

`7\text{ cm.}`

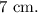
And the length of the rectangle is

`x+4=7+4=11\text{ cm.}`

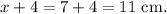
Final answer:

Hence the final answer is

`7\text{ cm and }11\text{ cm.}`