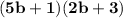
1) Let's factor completely this 2nd-degree polynomial, rewriting that 17b as the sum of two terms.
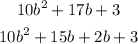
2) Now, let's group those factors and rewrite that as a product, placing outside the parentheses the GCD. Grouping the terms whose coefficient share the same
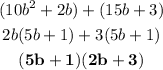
Thus this is the answer (in bold).