Observe the given figure carefully.
Consider the triangle ABE.
Since the angle formed at vertex A is a square angle, that is 90 degrees. So ABE must be a right triangle. Also, it is clearly visible that the side AE and AB are unequal. Also, we know that hypotenuse is the largest side of a right triangle, so it cannot be equal to either of the other two sides. So it can also be claimed that ABE is a scalene triangle.
Consider the triangle BEC.
Since all the angles formed by the sides of the triangle at vertices are less than 90 degrees, it can be claimed that BEC is an acute triangle. Also, note that,
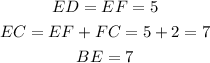
So we see that the sides BE and EC of the triangle are equal, therefore, BEC will be an isosceles triangle.
Consider the triangle DEF.
From the diagram, it is clearly seen that,

Since all three sides of the triangle measure equal, so DEF must be an equilateral triangle. Also, note that the angles formed by the sides at the vertices of the triangle are all 60 degrees that is less than 90 degrees. So DEF can also be designated as Acute Triangle.
Consider the triangle CDF.
In the triangle, the side DF measures 5 units, side CF measures 2 units. Also, it can be observed that the angle CFD is greater than 90 degrees. So CDF must be an obtuse triangle.
We just saw that side CF and DF are unequal. The side CD being opposite to the obtuse angle, is the largest side of the triangle, so it cannot be equal to either CF or DF. Therefore, triangle CDF must be a Scalene Triangle.
Thus, it is obtained that,
Triangle ABE is a right triangle and scalene triangle.
Triangle BEC is an acute triangle and isosceles triangle.
Triangle DEF is an acute triangle and an equilateral triangle.
Triangle CDF is an obtuse triangle and a scalene triangle.