Part e
we have the function
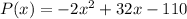
The given function represents a vertical parabola, open downward
The vertex represents a maximum
so
Convert the given equation into vertex form
step 1
Factor -2
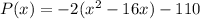
step 2
Complete the square
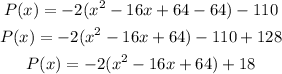
step 3
Rewrite as perfect squares
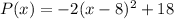
The vertex is the point (8,18)
That means
8 is the number of games in hundreds -------> 800 games
18 is the profit in ten thousand ------> 18*10,000=$180,000
so
The maximum profit is $180,000 for 800 games