Question

Which of the following is the least at x=9? B is sthaller than A & À whenx=9 2=7 (ostb 17 y=x+b Function A Function B 2 X Y y = 3x+6 0 -2 3 3 3 1 Y=12 6 4 9 7

Answer 1

You know that the Function A is:

`y=(2)/(3)x+6`

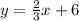
Substitute the given value of "x" into the Function A:

`\begin{gathered} y=(2)/(3)x+6 \\ \\ y=(2)/(3)(9)+6 \end{gathered}`

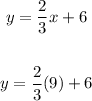
Evaluating, you get:

`\begin{gathered} y=(18)/(3)+6 \\ \\ y=6+6 \\ \\ y=12 \end{gathered}`

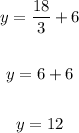
Given the Function B shown in the table, you need to identify the Input value 9 (or the x-value) and its corresponding Output value (or y-value).

In this case, when the value of "x" is:

`x=9`

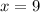
The value of of "y" is:

`y=7`

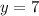
Since the Output value in Function B is less than the the Output value in Function A when the value of "x" is 9, you can determine that the the answer is: