The question requires us to calculate the mass of an insoluble solid given the following information:
Volume of liquid + Volume of solid = V(liq) + V(sol) = 91.0 mL
Density of liquid = d(liq) = 0.865 g/mL
Density of solid = d(sol) = 3.50 g/mL
Mass of liquid = m(liq) = 48.8 g
To solve this question, we must use the definition of density (ratio between mass and volume):

We'll follow the steps to solve the question:
1) Calculate the volume of liquid, considering its mass and density;
2) Calculate the volume of solid, considering the total volume given and the calculated volume of liquid;
3) Calculate the mass of solid, considering the given density and calculated volume.
First, we need to rearrange the density formula to calculate the volume of liquid considering the mass and density provided:

Now that we have the calculate volume of the liquid (56.4 mL), we can use the total volume provided to calculate the volume of the solid:
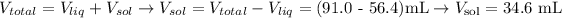
With the volume of the insoluble solid calculated (34.6 mL), we can use the density given (3.50 g/mL) and obtain the mass of the solid, using the formula for density rearranged:
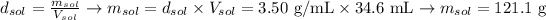
Therefore, the mass of the insoluble solid should be 121.1 g.