Given 5 roses, 8 daisies, 7 lilies, and 5 orchids.
Total number of flowers = 5 + 8 + 7 + 5 = 25 flowers
Total number of flowers minus rose = 8 +7 + 5 =20 flowers
If 4 flowers are selected and not replaced, the probability that at least one of the flowers is a rose
The probability formula is:
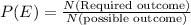
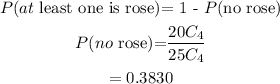
Therefore,
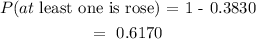
The Probability that at least one of the flowers is a rose is 0.617