Question

How would I set up my equation for letter b and c?

Answer 1

d) Recall that by the exterior angle theorem we know that:

`a+b=d\text{.}`

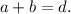
Therefore,

`5x+10+6x+2=12x\text{.}`

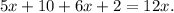
Adding like terms we get:

`11x+12=12x\text{.}`

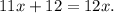
Subtracting 11x from both sides of the equation we get:

`\begin{gathered} 11x+12-11x=12x-11x, \\ 12=12x-11x, \\ x=12. \end{gathered}`

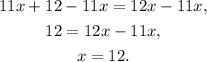
Therefore, we get that:

`d=12x=12(12)=144.`

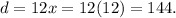
Recall that c and d are a linear pair, meaning:

`\measuredangle c+\measuredangle d=180^(\circ).`

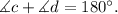
Substituting d= 180 degrees and solving for angle c we get:

`\measuredangle c=180^(\circ)-144^(\circ)=36^(\circ).`

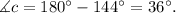
Answer part d):

`\begin{gathered} x=12, \\ \measuredangle c=36^(\circ). \end{gathered}`

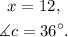
c) To solve this question we will use the fact that the interior angles of a triangle add up to 180 degrees, and that h and i are a linear pair.

Since the interior angles of a triangle add up to 180 degrees, then:

`\measuredangle k+\measuredangle j+\measuredangle h=180^(\circ).`

Solving the above equation for angle h we get:

`\measuredangle h=180^(\circ)-\measuredangle j-\measuredangle k.`

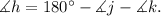
Substituting ∡j=42°, ∡k=50° we get:

`\measuredangle h=88^(\circ).`

Now, since angles h and i are a linear pair, then:

`\measuredangle h+\measuredangle i=180^(\circ).`

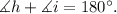
Solving for angle i we get:

`\measuredangle i=180^(\circ)-\measuredangle h=180^(\circ)-88^(\circ)=92^(\circ).^{}`

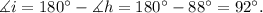
Finally, we know that:

`\measuredangle i+\measuredangle n+\measuredangle m=180^(\circ).`

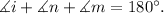
Substituting the measures of angles i, and n, and solving for m we get:

`\measuredangle m=180^(\circ)-92^(\circ)-33^(\circ)=55^(\circ).^{}`

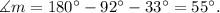
Answer part c):