Ms. Shank ran 5 2/7 miles.
Mr. Jones ran 4 3/4 miles.
To determine how much farther did Ms. Shank ran than Mr. Jones, you have to calculate the difference between both distances:

To calculate this difference, you can calculate the difference between the whole numbers and the difference between the fractions separately:
- Difference between whole numbers:
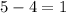
- Difference between fractions:

First, you have to express both fractions with the same denominator, the least common factor between "7" and "4" is 28, multiply the first fraction by 4 and the second by 7 to express both of them as their equivalent with denominator 28:
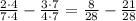
Now that both fractions have the same denominator you can calculate the difference between them:

- The final step is to add the results of the difference between the whole numbers and the fractions:
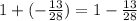
Divide the whole number by 1 to express it as a fraction, then, multiply the fraction by 28. Once both fractions have the same denominator, you can calculate the difference
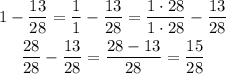
Ms. Shank ran 15/28 miles more than Mr. Jones.