Question

Which of the following equations have complex roots?A. 3x² + 2 = 0B. 3x2 - 1 = 6xC. 2x2 - 1 = 5xD. 2x + 1 = 7x

Answer 1

Given:

There are 4 equations.

To find:

The complex roots.

Step-by-step explanation:

A) Considering option A,

`3x^2+2=0`

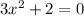
Let us find the discriminant value.

`\begin{gathered} \Delta=b^2-4ac \\ =0-4(3)(2) \\ =-24<0 \end{gathered}`

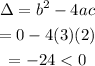
Since it is negative. So, it has complex roots.

B) Considering option B,

`\begin{gathered} 3x^2-1=6x \\ 3x^2-6x-1=0 \end{gathered}`

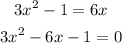
Let us find the discriminant value.

`\begin{gathered} \Delta=b^2-4ac \\ =(-6)^2-4(3)(-1) \\ =48>0 \end{gathered}`

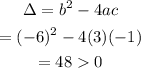
Since it is positive. So, it has real roots.

C) Considering option C,

`\begin{gathered} 2x^2-1=5x \\ 2x^2-5x-1=0 \end{gathered}`

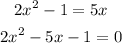
Let us find the discriminant value.

`\begin{gathered} \Delta=b^2-4ac \\ =(-5)^2-4(2)(-1) \\ =33>0 \end{gathered}`

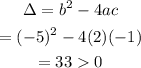
Since it is positive. So, it has real roots.

D) Considering option D,

`\begin{gathered} 2x+1=7x \\ 5x=1 \\ x=(1)/(5) \end{gathered}`

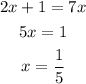
So, it has a real solution.

Final answer:

Option A has complex roots.