Given:
The required angle is in the first quadrant with position P(u,v) = (3,4)
Let us begin by showing the position of the angle using the given position:
Using trigonometric ratios, we can solve for theta as shown:
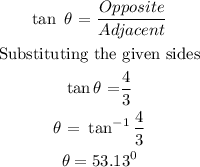
Solving for the required angle:

The result is equivalent to -24/7.
Answer: -24/7 (Option 3)