As per given by the question,
There are given that a length of three sides of the triangle.
The length of sides are, 14cm, 22cm, and 30cm.
Now,
For finding the measure of the smallest angle,
The smallest angle in a triangle is always opposite the shortest side. and also the bigest angle is always opposite the longest side.
So,
Suppose length A is 14cm, B is 22 cm and C is 30cm.
Then,
From the law of cosines,
Let A be the smallest angle.
So,
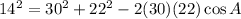
Now,
Find the value of angle A,
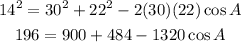
Now,

Then,
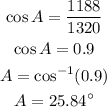
Hence, the measure of the smallest angle is 25.84 degree.