Question

Hello! I need help finding the 2 roots of the equation other than 1 and 2 please!!

Answer 1

You know that a polynomial can be writen in function of it's roots like:

`ax^4+bx^3+cx^2+dx+e=(x-x_1)(x-x_2)(x-x_3)(x-x_4)`

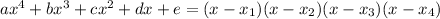
x1, x2, x3 and x4 are the roots. So you have that 1 and 2 are roots, so part of the polynomial is:

`(x-1)\cdot(x-2)=x^2-3x+2`

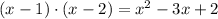
If this 2 degree polynomial represent's 2 of the 4 roots of the original polynomial, it means that the original one can be divided by this one. Notice that if we do that, we will get a 2 degree polynomial, which roots are very easy to find. Let's divide:

So, the new polynomial you have to find the roots of is:

`12x^2+x-1`

Now for this one is very easy. We just use the formula:

`\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where a, b and c are the coefficients of the polynomial:

`ax^2+bx+c`

For our polynomial, a = 12, b = 1 and c = -1. Let's call this new roots x3 and x4:

`x_3=\frac{-1+\sqrt[]{1^2-(4\cdot12\cdot(-1))}}{2\cdot12}=\frac{-1+\sqrt[]{1+48}}{24}=\frac{-1+\sqrt[]{49}}{24}=(-1+7)/(24)=(1)/(4)=0.25`
`x_3=\frac{-1-\sqrt[]{1^2-(4\cdot12\cdot(-1))}}{2\cdot12}=\frac{-1-\sqrt[]{1+48}}{24}=\frac{-1-\sqrt[]{49}}{24}=(-1-7)/(24)=-(1)/(3)\cong0.333`

So, the roots of the given polynomial, other than 1 and 2, are 1/4 and 1/3