The function given in the question is
![v(t)=\frac{1+\sqrt[]{t+9}}{\sqrt[]{t+9}}](https://img.qammunity.org/2023/formulas/mathematics/college/j0mbao7uywe1c6r12op6oulp2yye99tibc.png)
Concept: To calculate the particle position of the function above, we will have to find the anti-derivative of the function above
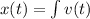
By substituting the values, we will have
![\begin{gathered} x(t)=\int v(t) \\ x(t)=\int \frac{1+\sqrt[]{t+9}}{\sqrt[]{t+9}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gxckfemn3xc1kt0913znbzw82a3za8y5pb.png)
Step 1: Spilt the function using the law of integration of addition
![\int \frac{1+\sqrt[]{t+9}}{\sqrt[]{t+9}}=\int \frac{1}{\sqrt[]{t+9}}+\int \frac{\sqrt[]{t+9}}{\sqrt[]{t+9}}](https://img.qammunity.org/2023/formulas/mathematics/college/f28ijbs2sons7qnyxkh2ybdoag3ny1hgkd.png)
Step 2: The equation above becomes
![\int \frac{1}{\sqrt[]{t+9}}+\int \frac{\sqrt[]{t+9}}{\sqrt[]{t+9}}=\int \frac{1}{\sqrt[]{t+9}}+\int 1](https://img.qammunity.org/2023/formulas/mathematics/college/apuaxu44kfyced1cfmnlsa7g48w5ed5mrt.png)
Step 3: Integrate the expression below using integration by substitution
![\begin{gathered} \int \frac{1}{\sqrt[]{t+9}}dt \\ \text{let } \\ u=t+9 \\ (du)/(dt)=1 \\ du=dt \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d0qsirpej5h2pwa4be21v4os3ywx8ye5mr.png)
![\begin{gathered} \int \frac{1}{\sqrt[]{u}}du=\int u^{-(1)/(2)}du=\frac{u^{-(1)/(2)+1}}{-(1)/(2)+1}=u^{(1)/(2)}/(1)/(2)=2u^{(1)/(2)}=2\sqrt[]{u}=2\sqrt[]{t+9} \\ \int 1=t \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uljtrcyj6gc7191z9yv3b0pgfsurqhj9fa.png)
![\int \frac{1}{\sqrt[]{t+9}}+\int 1=2\sqrt[]{t+9}+t+c](https://img.qammunity.org/2023/formulas/mathematics/college/43lubglv4c6e9h1izrqi9vfbufw8r226fz.png)
![x(t)=2\sqrt[]{t+9}+t+c](https://img.qammunity.org/2023/formulas/mathematics/college/7ms5wbwpzg5xdcb6th4z9oulu7fdpp2lxb.png)
To calculate the value of constant c., since it is starting from the origin, we will have
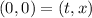
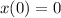
![\begin{gathered} x(t)=2\sqrt[]{t+9}+t+c \\ 0=2\sqrt[]{0+9}+0+c \\ 0=2\sqrt[]{9}+c \\ 0=6+c \\ c=0-6 \\ c=-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3qe3wqjuse94mzeor7qvlh9qv47yy2zllf.png)
Replace the value of c in the function of x(t)
![\begin{gathered} x(t)=2\sqrt[]{t+9}+t+c \\ x(t)=2\sqrt[]{t+9}+t-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5fe7ziuk6f4g37t7qqe8jnk6ufaw2ajton.png)
At t=16, we will have the particle position be
![\begin{gathered} x(t)=2\sqrt[]{t+9}+t-6 \\ x(16)=2\sqrt[]{16+9}+16-6 \\ x(16)=2\sqrt[]{25}+10 \\ x(16)=2*5+10 \\ x(16)=10+10 \\ x(16)=20 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w55on4baewlritju7zux6wygg9r8t3fo2x.png)