Given that the mass of clown 1 is m1 = 55.5 kg
Mass of clown 2 is m2 = 72.5 kg
The initial velocity of clown 1 is
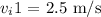
The initial velocity of clown 2 is zero as it is at rest.
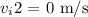
After the collision, the mass of the clown will be added up as they are stuck together.
So, the mass after the collision will be
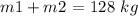
According to conservation of momentum,
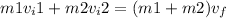
Here, v_f is the final velocity that is after the collision.
Substituting the values, the final velocity will be
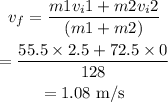
Kinetic energy lost during this process will be
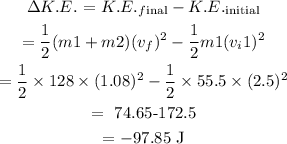
Here, the negative sign indicates the loss in kinetic energy.
Thus, 97.85 J kinetic energy is lost during this process.