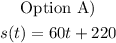Question

In 2008, a school’s enrollment was 400 students. In 2012, the school’s enrollment was 640 students. Which linear model represents the school’s enrollment, s, as a function of t, the number of years after 2005?

A. s(t)=60t+220
B. s(t)=220t+60
C. s(t)=4t+240
D. s(t)=240t+4
E. s(t)=60t
F. s(t)=240t

Answer 1

Since we should use a linear model, write the equation of a line that passes through two given points.

Since time is measured as the number of years after 2005, then, the point (3,400) represents that in 2008, the enrollment was 400 students. The point (7,640) represents that in 2012 the enrollment was 640.

Use the slope formula to find the slope of the linear model:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ =(640-400)/(7-3) \\ =(240)/(4) \\ =60 \end{gathered}`

The equation for a linear model with slope m and y-intercept b is:

`s(t)=mt+b`

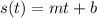
Since m=60, then the linear model that suits the situation is:

`s(t)=60t+b`

Substitute t=3 and s(3)=400 to find the value of b:

`\begin{gathered} s(3)=60(3)+b \\ \Rightarrow400=180+b \\ \Rightarrow400-180=b \\ \therefore b=220 \end{gathered}`

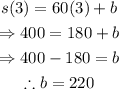
Substitute b=220 to find the complete expression for the linear model:

`s(t)=60t+220`

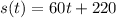
Therefore, the answer is:

`\begin{gathered} \text{Option A)} \\ s(t)=60t+220 \end{gathered}`