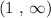
Step-by-step explanation:
Since for g(-∞), is not a possible answer. we remove it.
We also remove (∞,∞), because it goes back to being simply ∞.
Now for
(0 , 1 )
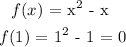
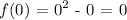
This is not positive, nor negative so we will also put this one on the side.
For the last interval (1, ∞)
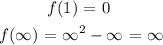
=> f(x) is positive
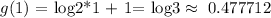
g(1) is positive
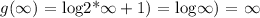
=> g(∞) is positive
Hence f(x) and g(x) are both positve on the interval (1, 8)
NB:
Technically you should say g(x) tend to infinity (or a approaches infinity) not is equal to infinity, because infinity is not a number