Question

Let x be a continuous random variable that follows a normal distribution with a mean of 450 and a standard deviation of 80.Find the value of x so that the area under the normal curve between pand x is approximately 0.4591 and the value of x is greater than the mean? Round your answer to the nearest integer.

Answer 1

In order to calculate the value of x, first we need to find the value of z such as the area between the mean and x is 0.4591.

Looking at the z-table, the value of z that gives this area is z = 1.74

Then, using the formula for z, we can calculate the value of x:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ 1.74=(x-450)/(80) \\ x-450=139.2 \\ x=589.2 \end{gathered}`

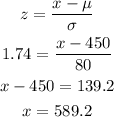
Rounding to the nearest integer, we have x = 589.