From the table, we were given the zero of the function h(x).
The zeros of the function are
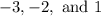
The formula to obtain the equation of the function is,
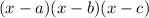
Where
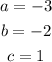
Hence,
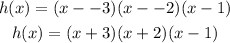
Expanding the function above
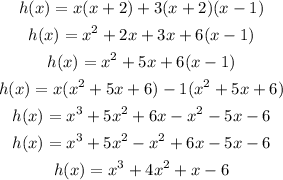
Therefore, the equation of the polynomial function is

Hence, the answer is Option 3.