Question

Solve the exponential equation 2^x=3(a) Express the solution set so that the solution is in exact form. Express your answer using either log of In.(b) If the solution is irrational, approximate the solution to the nearest thousandth.

Answer 1

Step-by-step explanation:

To solve exponential equations we have to use the properties of the logarithms:

`2^x=3`

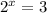
First we apply log on both sides of the equation:

`\log (2^x)=\log (3)`

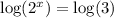
Now we use the logarithm of a power property:

`\log (a^b)=b\log (a)`

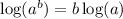
For this equation:

`x\log (2)=\log (3)`

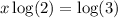
And divide both sides by log(2):

`x=(\log (3))/(\log (2))\approx1.585`

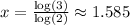
Anwers:

• (a) ,x = log(3)/log(2)

,

• (b) ,x = 1.585