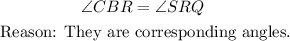The Solution:
Based on the diagram given in the question, we provide the following answers:
a. The type of construction demonstrated in the given diagram is the construction of two parallel lines ( that is, line BC and RS ).
Representing the geometric relationship in the construction, we that line BC is parallel to line RS. Symbolically, it is

b. The conjecture that can be determined from the construction is that angle B is equal to angle R. That is,
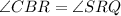
c. Justifying the above conjecture, we have