Question

Brand A granola is 25% nuts and dried fruit and brand B granola is 10% nuts and dried fruit. How much of sweet item A and sweet item B should be mixed to form a 10-lb batch ofsweets that is 16% nuts and dried fruit?The batch of sweets should contain lb of Brand A granola and lb of Brand B granola

Answer 1

We have to find the mix of brand A and brand B to make 10 lb of a mix that have the specific percentage of nuts and dried fruit (16%).

Lets call A the mass of brand A in the mix and B the mass of brand B in the mix.

We can write two equations with the information given:

- The total mass of the mix, that will be the sum of the mass of A and the mass of B and will total 10 lb:

`A+B=10`

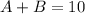
- The total amount of nuts and dried fruit. In this case, it will be the sum of the absolute amount of nuts dried fruit in A and the absolute amount of nuts and dried fruit in B. We can find this absolute value by multiplying the relative value (the percentage given, in decimal form) by the mass of each brand. This sum will total the absolute value of nuts and dried nuts in the mix, also equal to the percentage of nuts and dried fruits in the mix multiplied by the total mass:

`\begin{gathered} 0.25\cdot A+0.10\cdot B=0.16\cdot10 \\ 0.25A+0.10B=1.60 \end{gathered}`

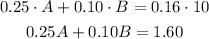
Now, we have a system of two equations and two unknowns.

We can solve it by substitution, by clearing B from the first equation and replacing it in the second equation:

`A+B=10\Rightarrow B=10-A`
`\begin{gathered} 0.25A+0.10B=1.6 \\ 0.25A+0.10(10-A)=1.6 \\ 0.25A+1-0.10A=1.6 \\ (0.25-0.10)A=1.6-1 \\ 0.15A=0.6 \\ A=(0.6)/(0.15) \\ A=4 \end{gathered}`
`B=10-A=10-4=6`

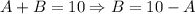
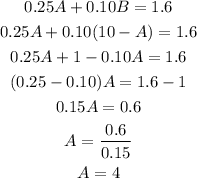
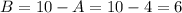
Answer:

The batch of sweets should contain 4 lb of Brand A granola and 6 lb of Brand B granola.