Question

Given parallelogram ABCD, angle D = 4x + 4, and angle C = 6x + 6, find angle A. (Please note, canvas is broken so I had to rewrite it.)

Answer 1

`m\angle A=108`

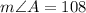
Step-by-step explanation

`\begin{gathered} m\angle D=4x+4 \\ m\angle C=6x+6 \\ m\angle A? \end{gathered}`

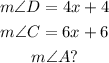
Step 1

A parallelogram is a quadrilateral whose opposite sides are parallel. The opposite angles of a parallelogram are equal

`m\angle A=m\angle C\rightarrow equation(1)`

Also,the sum of any two adjacent angles of a parallelogram is equal to 180°

`\begin{gathered} \text{blue angle(1)+yellow angle(2)}=180 \\ m\angle D+m\angle C=180\rightarrow equation(2) \\ \text{replace} \\ (4x+4)+(6x+6)=180 \\ 10x+10=180 \\ \text{subtract 10 in both sides} \\ 10x+10-10=180-10 \\ 10x=170 \\ \text{divide both sides by 10} \\ (10x)/(10)=(170)/(10) \\ x=17 \end{gathered}`

Step 2

use the equation(1) to find angle A

`\begin{gathered} m\angle A=m\angle C\rightarrow equation(1) \\ \text{replace} \\ m\angle A=6x+6 \\ \text{replace the x value} \\ m\angle A=6\cdot17+6=102+6 \\ m\angle A=108 \end{gathered}`

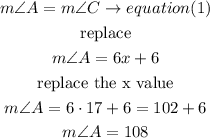
I hope this helps you