Consider the upper triangle
if we want to find b side, consider the following trigonometric identity:
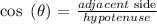
in this case, we have:
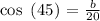
solve for b:
![b\text{ = cos(45) x 20 = }\frac{\sqrt[]{2}}{2}\text{ x 20 = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/wjr4uda3a4jo4dvvspnqt1d6tx43k0qvqm.png)
then, we can conclude that
![b\text{ = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/cgnkgz3zhga3qjbl18v49e8x4og3e2r5h8.png)
Now, for a-side, consider the following trigonometric identity:
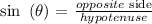
in this case, we have:
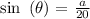
solve for a:
![a\text{ = }\sin \text{(45) x 20 = }\frac{\sqrt[]{2}}{2}\text{ x 20 = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/esom9v3xeo46x8evtobhjpn59j51az4pa6.png)
then, we can conclude that
![a\text{ = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/52xmgalpmevunyx1q3j03yegeay7izjxor.png)
Now, for the c-side, consider the greater triangle :
if we denote the hypotenuse by h, then by Pythagorean theorem we have:
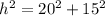
but h = a + c, then, replacing this in the previous equation we have
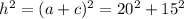
but, we know that a is
![a\text{ = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/52xmgalpmevunyx1q3j03yegeay7izjxor.png)
then we have:
![(10\sqrt[]{2}+c)^2=20^2+15^2\text{ = 625}](https://img.qammunity.org/2023/formulas/mathematics/college/bugzcjykwfgginrt7j5ik2qk6gbu3op56v.png)
now, taking the square root of both sides of the equation we obtain:
![10\sqrt[]{2}+c^{}=\text{ 25}](https://img.qammunity.org/2023/formulas/mathematics/college/zh64mbipos46wkjkbvgnw5a5xgs3irn8et.png)
solve for c:
![c^{}=\text{ 25}-\text{ 10}\sqrt[]{2\text{ }}\text{ }\approx10.85](https://img.qammunity.org/2023/formulas/mathematics/college/xkpsdxg7ug666bietv2at1n1poqrlmtd9y.png)
then we can conclude that :
![a\text{ = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/52xmgalpmevunyx1q3j03yegeay7izjxor.png)
![b\text{ = 10}\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/cgnkgz3zhga3qjbl18v49e8x4og3e2r5h8.png)
and
![c^{}=\text{ 25}-\text{ 10}\sqrt[]{2\text{ }}\text{ }\approx10.85](https://img.qammunity.org/2023/formulas/mathematics/college/xkpsdxg7ug666bietv2at1n1poqrlmtd9y.png)