We want to calculate the sticker price. The sticker price is given by the formula
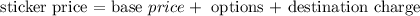
We are told that the destination charge is 476. We should determine the base price and the options to find the price sticker.
We are told that the dealer's cost of the base price is 92% of the pase price. So we have the equation
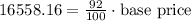
so if we divide both sides by 92 and multiply by 100 we get
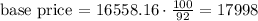
Now, applying the same principal for the options, we have

which means that
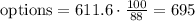
Replacing these values in the original equation we have that
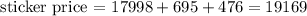
so the sticker price would be 19169