Given:
Initial deposit = $8500
rate of interest = 5% compounded annuallly
time (t) = 6 years
If Ao is invested at an annual interest rate r and compounded semiannually, the amount At after t years is given by the formula:

The compound amount in 6 years:
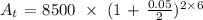
Simplifying we have:
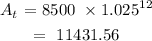
Answer:
$11431.56