1 Answer

Dan Fitch · Answer 1 · 2023-07-26T14:15:04+0000

In order to find the margin of error, we need to know that the width of the confidence interval is equal to 2 times the margin of error.

The width of this confidence interval is given by:

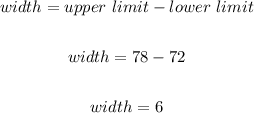
$\begin{gathered} width=upper\text{ }limit-lower\text{ }limit\\ \\ width=78-72\\ \\ width=6 \end{gathered}$

If the width is 2 times the margin of error, we have:

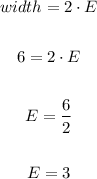
$\begin{gathered} width=2\cdot E\\ \\ 6=2\cdot E\\ \\ E=(6)/(2)\\ \\ E=3 \end{gathered}$

The margin of error is equal to 3, therefore the correct option is D.

Please log in or register to add a comment.